Сети данных

Рассмотрим основную структуру данных, которая появляется при структурном программировании. Учет этой структуры позволяет преобразовать благие пожелания о согласованности информационных потоков и хода передач управления в достаточно строгую методику.

Сеть данных может быть формально описана как ациклический ориентированный граф, в котором все ко-пути (т. е. пути, взятые наоборот) конечны и вершинам которого сопоставлены значения.

Рассмотрим пример. Известному стандартному приему программирования в языках без кратных присваиваний - обмену двух значений через промежуточное

z := second; second := first; first := z;

соответствует следующая сеть данных:

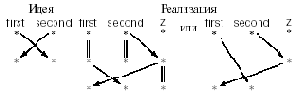
Рис. 14.1.1. Обмен значений

Здесь first, second, z можно считать комментариями, а сами данные опущены, поскольку их конкретные значения не важны.

На этом примере видно, что порой для лучшего структурирования сети целесообразно вводить дополнительные вершины, соответствующие сохраняющимся значениям. Ребро, ведущее из одной такой вершины в другую, обозначается при помощи стрелочки, похожей на равенство. Видно так же, как материя воздействует на идею, заставляя вводить дополнительные операторы и дополнительные значения. В данном случае переменная z и включающие ее операторы являются подпорками, и, если их исключить, сеть данных становится проще. Но в общераспространенных языках программирования нет кратных присваиваний типа

first,second:=second,first;

Даже если бы они были, представьте себе, как неудобно станет читать длинное кратное присваивание и понимать, какое же выражение какой переменной присваивается!

В случае программы вычисления факториала7) сеть потенциально бесконечна вниз, поскольку аргументом может быть любое число, но по структуре еще проще:

Рис. 14.1.2.

Перекрестных зависимостей между параметрами нет, следовательно, возможны две известные реализации факториала: циклическая и рекурсивная. Покажем их на разных языках, ибо все равно, на каком традиционном языке их писать.

function fact(n: integer): integer; var j,res: integer; begin res:=1; for j:=1 to n do res:=res*j; result:=res; end;

int fact(int n) {if (n==0) return(1); else return(n*fact(n-1));}

Схема построения циклической программы называется потоковой обработкой. Значения на следующей итерации цикла зависят от значений на предыдущей.

Для чисел Фибоначчи (та же схема (14.1.2)) структура уже несколько сложнее предыдущих, поскольку каждое следующее число Фибоначчи зависит от двух предыдущих, но метод потоковой обработки применим и здесь.

int fib(int n) {int fib1,fib2; fib1=1; fib2=1; if (n>2){ for (int i=2;i<n;i++){ int j; j=fib1+fib2; fib1=fib2; fib2=j; } }; return(fib2); }

Итак, в потоке изменяется структура из двух элементов. Ее можно было бы прямо описать как структуру данных, и это следовало бы сделать, будь программа хоть чуть-чуть посложнее. Тогда вместо подпорки j пришлось бы ввести в качестве подпорки новое значение структуры.

В программе имеется еще одна подпорка - параметр цикла i, который нужен лишь для формальной организации цикла.

Рекурсивная реализация чисел Фибоначчи пишется еще проще и служит великолепным примером того, как презренная материя убивает красивую, но неглубокую идею.

int fib(int n) { if (n<3) return(1); else return(fib(n-1)+fib(n-2)); }

Если n достаточно велико, каждое из предыдущих значений функции Фибоначчи будет вычисляться много раз, причем без всякого толку: результат всегда будет один и тот же! Зато все подпорки убраны...

В следующем примере неэффективность рекурсии по сравнению с хорошо организованным циклом еще более очевидная. Пусть надо найти путь, на котором можно собрать максимальное количество золота, через сеть значений, подобную показанной на рис. 14.1.

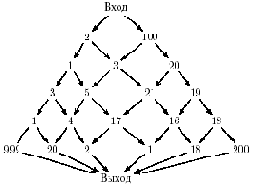
Рис. 14.1. Золотая гора

При циклической организации вычислений нам придется посчитать значение в каждой точке горы всего один раз (найти добычу на оптимальном пути в эту точку). Здесь используется то свойство оптимальных путей, которое делает возможным так называемые методы волны или динамического программирования: каждый начальный отрезок локально оптимального пути локально оптимален.

Это свойство является призраком, стоящим за эффективной циклической реализацией алгоритма, а многочисленные пути, соответственно, призрачными значениями, которые не нужно вычислять. В рекурсивной реализации мы не учитываем данного призрака, и он беспощадно мстит за вопиющее незнание теории.

Теперь рассмотрим случай, когда рекурсивная реализация намного изящнее циклической, легче обобщается и не хуже по эффективности8)

Рис. 14.1.3. Алгоритм Евклида

В данном случае путь для получения результата не разветвляется, и нам остается лишь двигаться по нему в правильном направлении (от цели к исходным данным) и достаточно большими шагами.

function Euklides(n,m: integer) integer; { предполагаем m<=n} begin if n=m then resut:=n else result:=Euklides(n mod m, m); end;

Если пытаться вычислить наибольший общий делитель методом движения от данных к цели, то нам придется построить громадный массив значений НОД, лишь ничтожная часть значений в котором будет нужна для построения результата. Затраты на вычисление каждого отдельного элемента в данном случае малы, а при обратном направлении движения повторный счет не возникает.

Алгоритм Евклида в простейшем случае моделирует ту ситуацию, которая появляется в задачах обработки рекурсивных структур, например списков. То, что в отдельных случаях возникает повторный счет, - небольшое зло, когда эти случаи редки и нерегулярны. Повторный счет возникает и в циклических программах, поскольку найти в большом массиве совпадающие элементы порою труднее, чем заново посчитать нужные нам значения. Именно поэтому рекурсия оказалась столь эффективным методом работы со списками и позволила построить адекватный первопорядковый фундамент для современного функционального программирования.

Рассмотрим два крайних случая движения по сети. Когда сеть представлена в виде структуры данных, естественно возникает метод ленивого движения по сети, когда после вычисления значений в очередной точке выбирается одна из точек, для которой все предыдущие значения уже вычислены, и вычисляются значения в данной точке.

Как видно, в частности на примере золотой горы, этот метод недетерминирован и в значительной степени может быть распараллелен. Но в конкретном алгоритме нам придется выбрать конкретный способ ленивого движения, и он может быть крайне неудачен: например, он будет провоцировать длительное движение в тупик, когда у нас есть короткий путь к цели. Даже в теоретических исследованиях приходится накладывать условия на метод ленивого движения, чтобы гарантировать достижение результата (см., например, теорему о полноте семантических таблиц в книге [20]).

Другой крайний случай движения по сети, когда сеть делится на одинаковые слои. Например, в сети (14.1.4)

Рис. 14.1.4. Полностью заменяемый массив

можно представить слой статическим массивом и вроде бы полностью забыть о самой сети. Забытый призрак мстит за себя, в частности, при необходимости распараллеливания вычислений, и предыдущий случай отнюдь не эквивалентен следующему.

Рис. 14.1.5. Постепенно заменяемый массив

Конечно же большая сеть данных становится необозримой. Справиться с нею можно, лишь разбив сеть на подсети. Таким образом, блоки программы соответствуют относительно автономным подсетям.

Еще Э. Дейкстра в книге [11] предложил в каждом блоке описывать импортированные и экспортируемые им глобальные значения. Но такая "писанина" раздражала хакеров и в итоге так и не вошла в общепризнанные системы программирования. Сейчас индустриальные технологии требуют таких описаний, но из-за отсутствия поддержки на уровне синтаксического анализа все это остается благими пожеланиями, так что, если хотите, чтобы Ваша программа была понятна хотя бы Вам, описывайте все перекрестные информационные связи!

Резюмируя вышеизложенное, можно сделать следующие выводы.

Сеть данных сама по себе в программу не переходит, в программу переходят лишь некоторые свойства сети в качестве призраков и некоторые куски сети в качестве реальных значений.
Программа определяется не только сетью данных, но и конкретной дисциплиной движения по этой сети.
В случае, если очередные слои сети, появляющиеся при движении согласно заданной дисциплине, примерно одинаковы и состоят из многих взаимосвязанных значений, у нас возникает циклическая программа.
В случае, если вычисление можно свести к вычислениям для независимых элементов сети, чаще всего удобней рекурсия.
Самый общий способ движения по сети - ленивое движение, когда мы имеем право вычислить следующий объект сети, если вычислены все его предшественники.
Структурное программирование нейтрально по отношению к тому, каким именно способом будет исполняться полученная программа: последовательно, детерминированно, недетерминированно, совместно, параллельно либо даже на распределенной системе, - поскольку сеть лишь частично предписывает порядок действий.
Конкретный выбор порядка действий в последовательной детерминированной программе является подпоркой, о которой постоянно забывают.Поэтому он чаще всего вредит при перестройке программы.

Внимание!

Поскольку структурное программирование отработано и преподается лучше всего, здесь появилась возможность остановиться на гораздо более глубоких и принципиальных вопросах, чем в других стилях. В частности, призраки и подпорки возникают везде, они не являются спецификой структурного программирования, это важнейшие понятия для спецификации, документации и перестройки любой нетривиальной программы.

Содержание раздела